Mutation of \(\tau_d\)-tilting pairs

Home | \(\tau_d\)-rigid pairs | Mutation

This website intends to help illustrate the paper \(\tau_d\)-tilting theory for Nakayama algebras [RV24].

Preliminary

We are working with linear Nakayama algebras with homogeneous relations, admitting a \(d\)-cluster tilting subcategory \(\mathcal{C}\). Specifically, for an algebraically closed field \(\mathbf{k}\), we are working with the algebras \(\Lambda(n,l)=\mathbf{k}\mathbb{A}_n/R^l\), where \(R\) is the arrow ideal of the quiver \(\mathbb{A}_n\) given by $$ n\longrightarrow n-1 \longrightarrow \cdots \longrightarrow 2 \longrightarrow 1 .$$ The indecomposable modules of \(\operatorname{mod}\Lambda\) are uniquely given through their support on \(\mathbb{A}_n\), which can be described as subintervals of \([1,n]\). Hence, they will be denoted by \(M(a,b)\), where \([a,b]\) is their support-interval.

For some more preliminary information on the \(d\)-cluster tilting subcategory of \(\Lambda(n,l)\) and the possibility of constructing your own \(\tau_d\)-rigid pair, visit here. Note that a strongly maximal \(\tau_d\)-rigid pair \((M,P)\) is a \(\tau_d\)-rigid pair of \(\mathcal{C}\) such that for any other \(\tau_d\)-rigid pair \((N,Q)\) we have \(|N|+|Q|\leq |M|+|P|\). We have shown that for \(\Lambda(n,l)\) a \(\tau_d\)-rigid pair \((M,P)\) is strongly maximal if and only if \(|M|+|P|=n\).

Mutation

The paper [RV24] only deals with the concept of mutation on a surface level, however as it bears witness of the over-arching structure we provide some of our findings here.

Let \((M,P)\) and \((M',P')\in \mathcal{C}\times \operatorname{proj}\Lambda\) be strongly maximal \(\tau_d\)-rigid pairs of \(\Lambda(n,l)\). If there exists a pair \((N,Q)\in\mathcal{C}\times\operatorname{proj}\Lambda\) that is a summand of both \((M,P)\) and \((M',P')\), and \(|N|+|Q|=n-1\), then \((M,P)\) and \((M',P')\) are mutations of each other.

The first observation we want to share is that the \(\tau_d\)-mutation graph of strongly maximal \(\tau_d\)-rigid pairs (sm-\(\tau_d\)-mutation graph for short) over \(\Lambda(n,l)\) is connected [RV, Proposition 6.10]. This is not true in general, see the following example:

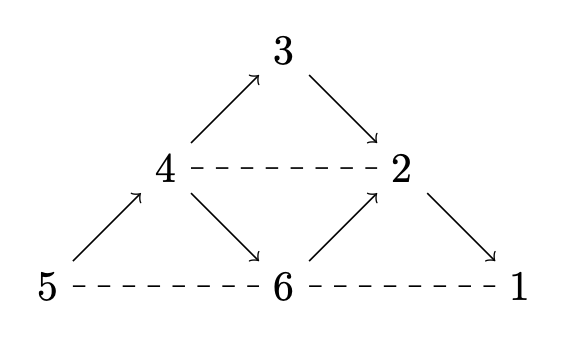
The sm-\(\tau_d\)-mutation graphs aren't necessarily connected. Consider for example the cyclic Nakayama algebra \(\Delta(3,7)=\mathbf{k}\tilde{\mathbb{A}}_3/R^7\), where \(\tilde{\mathbb{A}}_3\) is given by

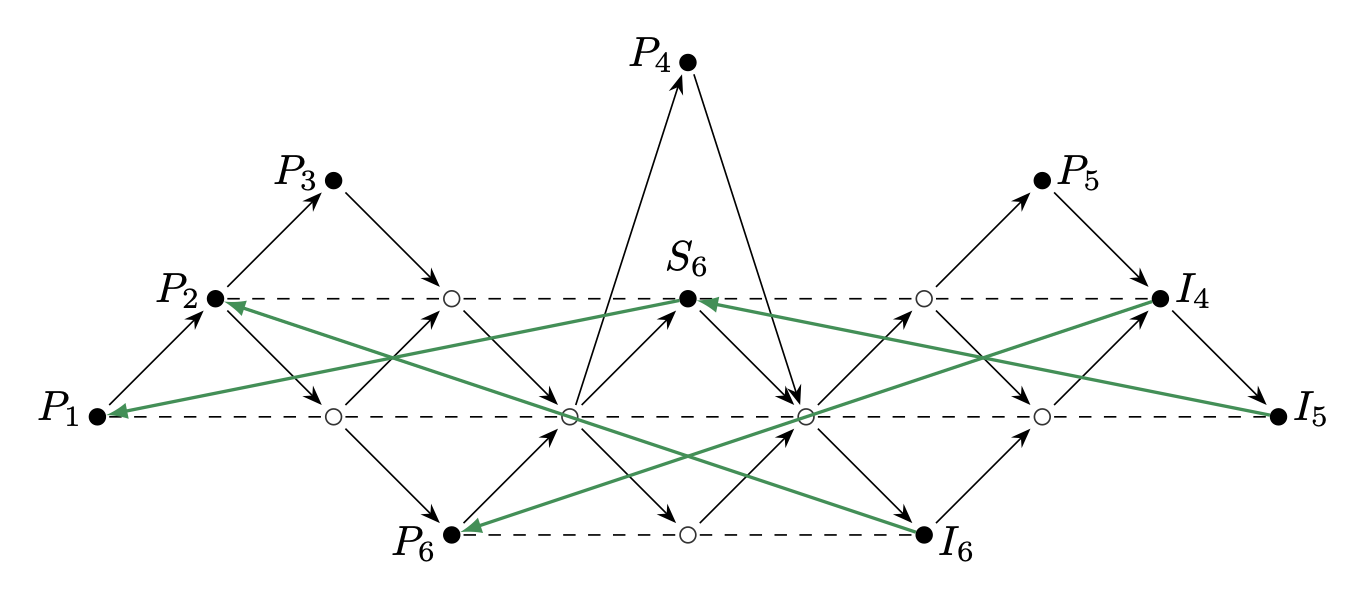
In \(\operatorname{mod}\Delta(3,7)\) we choose the \(2\)-cluster tilting subcategory \(\mathcal{C}\) given by the filled nodes in the AR-quiver below.

The sm-\(\tau_2\)-mutation graph of \(\mathcal{C}\) consist of two components:

We further showed that when \(\Lambda(n,l)\) is \(d\)-representation finite, the sm-\(\tau_d\)-mutation graph is an extended Dynkin graph of type \(\tilde{\mathbb{A}}\) with \(2n+l-1\) vertices [RV, Prop. 6.12]. This is not something that holds for \(d\)-representation finite algebras in general, a counterexample is given by the Auslander algebra of type \(\mathbb{A}_3\) (see further below).

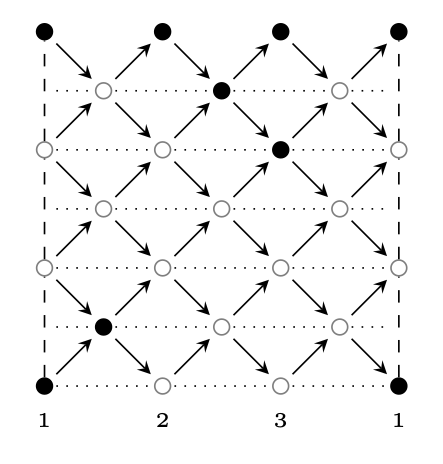
The sm-\(\tau_2\)-mutation graph of the \(2\)-representation finite algebra \(\Lambda(4,3)\) is

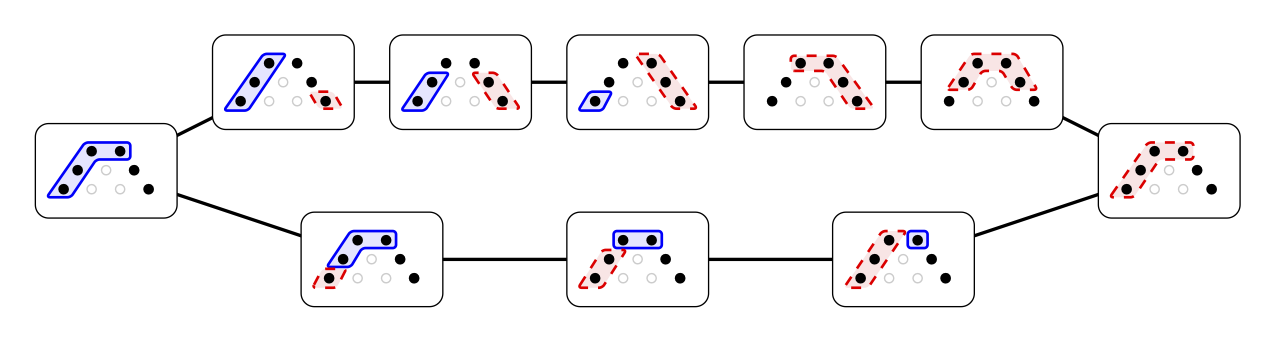
Even for \(\Lambda(n,l)\) the complexity of the sm-\(\tau_d\)-mutation graph increases quite rapidly when you move away from the \(d\)-representation finite case. Below we have included the sm-\(\tau_2\)-mutation graph of \(\Lambda(9,3)\) to exemplify this further below.

Mutate yourself!

Below you can generate an algebra \(\Lambda(n,l)\) which admit a \(d\)-cluster tilting subcategory, by choosing \(d\), \(p\) and \(l\) appropriately. The module category will be represented as it's AR-quiver where each vertex is an indecomposable. The darker vertices are indecomposables in the \(d\)-cluster tilting subcategory.

With a given \(\tau_d\)-rigid pair with \(n\) summands, you can choose a summand to mutate in. The summands which can be mutated will be displayed with a green or orange border, as well as an arrow. You can either choose to start with

1. the pair \((\Lambda,0)\),
2. the pair \((0,\Lambda)\), or
3. a pair \((M,P)\) of your choosing, given through a list of it's summands.

Nodes selected as a summand of \(M\) will be colored red, and nodes selected as a summand of \(P\) will be colored blue.

Mutation graph of \(\Lambda(9,3)\)

There are in total \(160\) different strongly maximal \(\tau_2\)-rigid pairs in the \(2\)-cluster tilting subcategory of \(\operatorname{mod}\Lambda(9,3)\). A pair here have at most \(6\) possible mutations and at least \(3\).
Click here to download pdf.

Mutation graph of the Auslander algebra of \(\mathbb{A}_3\)

We are now working over the algebra given by the following quiver with relations:

This is a \(2\)-representation finite algebra. The \(2\)-cluster tilting subcategory is given by the indecomposables marked with a filled circle in the following AR-quiver. We have also drawn the non-trivial actions of \(\tau_2\) on the indecomposables with green arrows.

There are in total \(40\) strongly maximal \(\tau_2\)-rigid pairs. The nodes in the sm-\(\tau_2\)-mutation graph have either 3 or 4 edges.
Click here to download pdf.